Consider the exceptionally simple process shown below in figure (a), where two feed streams are mixed together to produce a single product stream. Suppose that what is required is that the two feed streams shall have individually specified flowrates. A suitable control system for this would be as shown in figure (b).
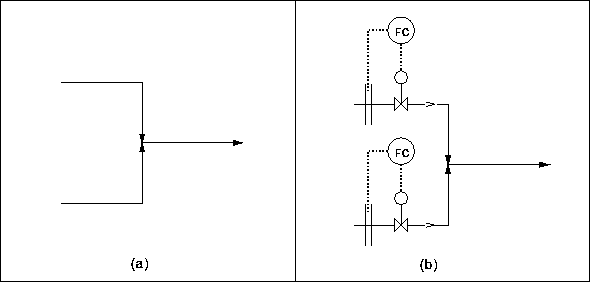
It should be immediately apparent that this control system is complete, i.e. we cannot put any more control loops on it. Having fixed two of the three streams which are connected together, conservation requires that the third must be the sum of these two.
This suggest the validity of the following rule.
Rule 1: `(n-1) out of n’. If n streams join together in a process or part of a process over which mass must be conserved (normally any process), then the flows of only ( n -1) of these may be set by flow controllers.
It is possible to prove this formally. As will be seen, further generalisation is also possible.
Conservation of mass requires that the sum of the inflow and outflows shall match over an extended period, but is it necessary to take steps to ensure that this happens from minute to minute? The flows would not always match if there were any possibility of material accumulating within the junction. This will not occur if the fluids are incompressible. This implies that it is necessary to have some mechanism to ensure that mass balances do actually balance. In this example, the design of the process, i.e. simple closed junction and incompressible fluid, ensures that this will be so.
However, consider what happens if we replace the closed junction by an open tank, see below figure (a). Here there is nothing to stop the tank from running dry or overflowing, unless, as in figure (b), we provide the tank with a level controller.
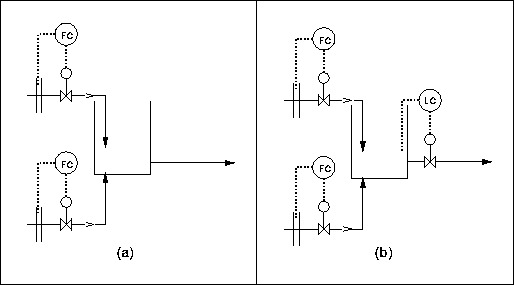
Rule 2 : Mass balances must balance. To ensure that mass balances do balance, there must either be an inplicit mechanism in the process, or an inventory controller must be supplied. The valve for the holdup control loop goes on the remaining stream.
Inventory or holdup is measured either by level or some equivalent measurement in a liquid system, or by pressure in a gas system. A simple junction with a liquid system is rather special in being `self regulating’ with respect to holdup.
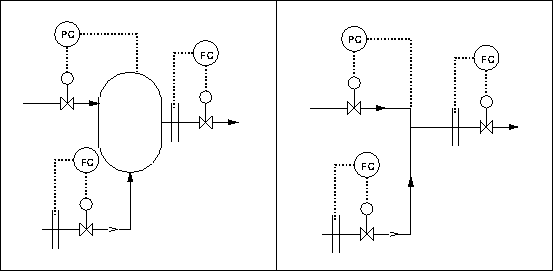
If we wished to regulate the total product rate from a simple mixing process and one only of the feeds, then we may require explicit holdup control for either compressible or incompressible fluids in either of the arrangements below. The vessel in the right hand figure is a closed vessel, which, in the case of a liquid system, would be run full. Whether or not a control loop for pressure is required will depend on the specific process conditions, in particular the source and sink pressures for the flows and the type of device, pump, compressor etc., if any, driving the flow.
Finally, there is a further rule implied by all these examples which really belongs before any of the others:
Rule 3: Strategic aims. The primary control objectives of a process are set by the strategic aims of the process. These define the basic control stucture.
Thus the fact that flow controllers were placed on the two feed streams in the first example and on the product and one feed in the last was a consequence of a decision by the process designer that these were the streams whose flows were to be fixed. It should thus be clear that the design of a process and of its control system cannot really be separated.