Proportional action is the simplest and most commonly encountered of all continuous control modes. In this type of action, the controller produces an output signal which is proportional to the error. Hence, the greater the magnitude of the error, the larger is the corrective action applied.
-
Mathematical Description
Mathematically, proportional control could be expressed as:
Where
- V is the adjustment or signal for the adjustment from the controller.
-
is the error. - = S - L
- L is the measured value of the controlled variable.
- S is the setpoint.
- K is the proportional constant, named as the gain which shows the sensitivity of the control.
-
Vo is the signal output when no error exists.The gain is often replaced with another parameter, called the proportional band, PB . This quantity is defined as the error required to move the final control element over its whole range and is expressed as a percentage of the total range of the measured variable. What is the relationship between K and PB .According to this definition we can see that the whole range of the final control element adjustment should be Vmin to Vmax .At point Vmin
At point Vmax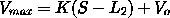 
The error required to move from Vmin to Vmax will be
Therefore
Recall that the proportional band, PB , is defined as the error required to move the final control element over it’s whole range expressed as a %. So for the controlled variable, L , with its total range Lmin to Lmax the definition for the proportional band is
or
Therefore we have the relationship between gain K and proportional band PB as
With proportional band, the relationship between the adjustment and the error can be expressed as
It can be seen both from the expression above and by running the experiments in the Virtual Laboratory that the larger the gain K , or equivalently the smaller the proportional band PB , the higher the sensitivity of the controller’s actuating signal to deviations will be.
-
Dynamic Response
Now let’s examine the dynamic response of the proportional control. Assume the process is at steady state and the level is at the setpoint. At time = 0, an increase in the inlet flowrate, regarded as a disturbance, enters into the process. If no control action is taken, i.e. the outlet flowrate is not altered, the level (controlled variable) will increase.
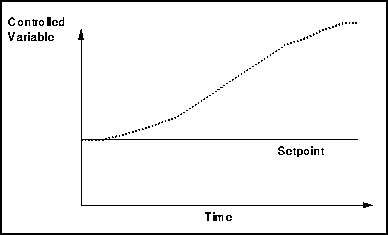
With proportional control, the level is brought back and maintained in a certain range near the setpoint. The history curve could typically be like that shown below. Different responses are obtained depending on the proportional band, B , of the controller.
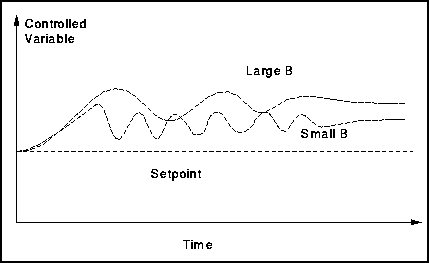
As can be seen the smaller the proportional band the closer to the setpoint the controlled variable becomes but the more oscillatory the response.
-
Advantages
The advantages of this type of controller are
- It is relativly simple and easy to design and tune
- It provides good stability
- It responds very rapidly
- Dynamically it is relatively stable
-
Disadvantages
From the response curve to a step change in the input two features should be noted. These are two points which make proportional control unsatisfactory.
- OffsetFor a sustained change of load, the controlled variable is not returned to the original or desired value, but attains a new equilibrium value termed control point. The difference between the control point and the desired value (set point)is referred to as offset.The reason for this offset with proportional action is that the control action is proportional to the error. Consider the above simple level control system. For the step increase in the flow of liquid into the tank, in order to maintain the level, the valve on the outlet must be opened wider. This will only occur if there is a continuous output from the controller. The output itself can only exist if there is an error signal supplied to the controller. In order to maintain this error, the level will rise above the desired level at the new control point, hence create an offset.
- OvershootThere is a significant time of oscillation, or in other words, overshoot. Although the period of this oscillation is moderate, this, in some cases, could be highly undesirable.