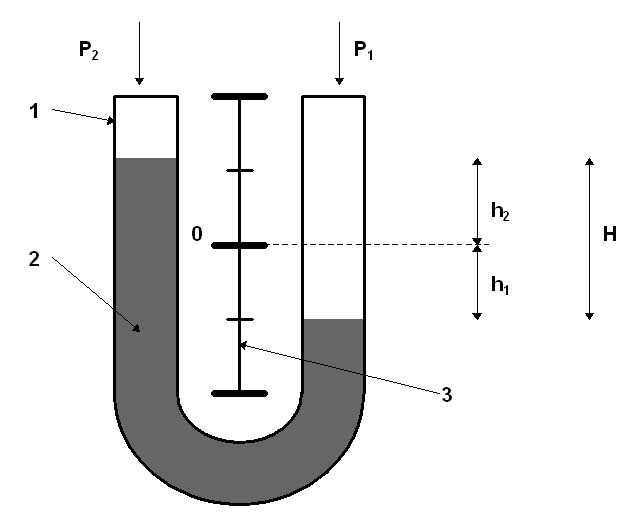
These manometers are used for measurement of gauge pressures (up to 0.1 MPa), vacuumetric pressures (down to 0.1 MPa below atmospheric pressure) and for differential pressures of liquids and gases.
The principle is based on the static balance between the measured pressure and the head of the liquid column. Fig. shows the schematic of this manometer. A glass tube 1, bended to the “U”-shape, is filled by one half of its volume with liquid 2 (water, mercury).

This tube is placed vertically, and a scale 3 (usually in mm) is attached along its height. Pressures P1 and P2 are supplied to legs of the tube, and levels of liquid in the legs change their position.When static balance between a measuring pressure and the head of the liquid column is reached, this pressure can be evaluated according to the equation:

where,
P1 and P2 - pressures supplied to the legs of the manometer,
Pa;h1 and h2 - deviations of liquid levels from the zero point of the scale in two legs of themanometer,
m;H= h1 + h2 - total length of the liquid column corresponded to the measuring differentialpressure,
m;ρ - density of liquid filled the “U”-tube,
kg/m3;gloc - local gravitational acceleration, m/s2.
Figure 1. Liquid filled “U”-tube manometer.
We need always make two readings of the liquid level, namely, in each leg of the tube, because in reality due to non-uniformity of the tube diameter along its length, values of h1 and h2 are not equal. As the result of such reading the error introduced during pressure measurement will be reduced. When this type of manometer is used for pressure measurements three cases may take place:
1). P1 is above atmospheric pressure, P2 = Patm. In this case the manometer measures the difference between absolute and atmospheric pressures: P1 = Pg = ρgloc(h1+h2)
2). P is below atmospheric pressure, P1 = Patm. In this case manometer measures the difference between atmospheric and absolute pressures: P2 = Pvac = ρgloc(h1+h2).
3). In this case the equation (3) refers to measurements of differential pressures.
Since the gravitational acceleration is used for the evaluation of pressure, then, when using “U”-tube manometers, it is necessary to introduce correction which takes into account the difference between gravitational acceleration in the place where this manometer was calibrated from that where it is used.Another source of the error is the deviation of liquid temperature in the tube from that temperature when this manometer was calibrated. Due to thermal expansion of the liquid in the tube the volume of liquid will change and this inevitably introduces an error.But the most common mistake is made by not correct reading the scale in respect to the meniscus of liquid in legs of the tube.
Fig. 2 gives examples how operator should make readings when using “U”-tube manometer with various liquids. We should always read a surface of the meniscus in its centre. In the case with water - in the bottom, and in the case with mercury - in the top of the meniscus. But in everyday industrial measurements the first two corrections (gravitational and thermal) are not always used, whereas the last one (the meniscus correction) must always be taken into account.
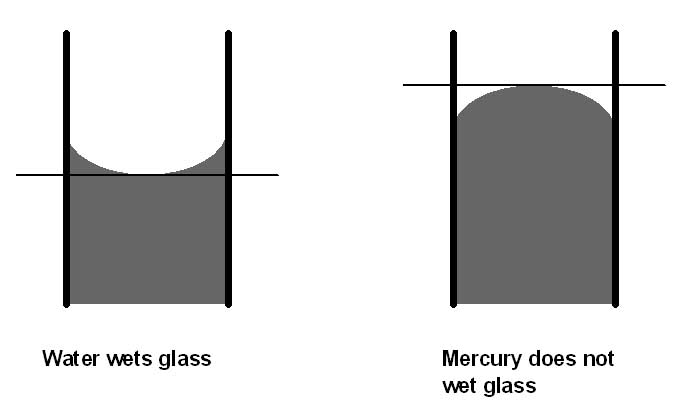
Figure 2. Correct reading of the “U”-tube manometer.