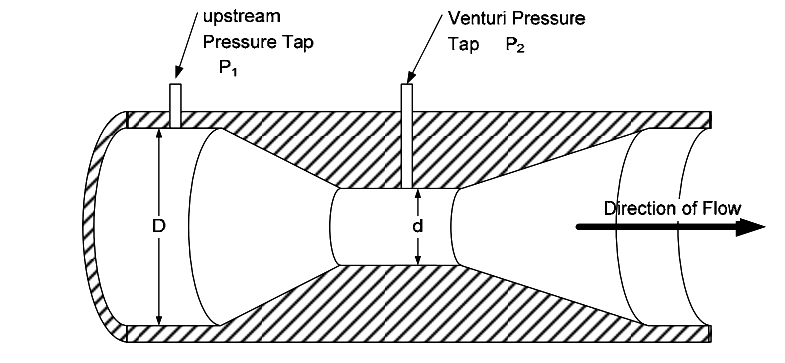
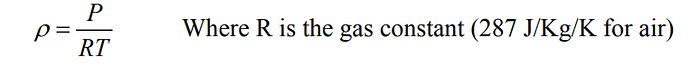The venturi flow meter, while considered an obstruction flow meter, is less of an obstruction than the orifice type. It still does have a certain amount of pressure drop, but it is significantly less than the orifice type meter.
Once again, as long as the incompressible fluid velocity is well below the supersonic point (< mach .3), the Bernoulli equation can be used.
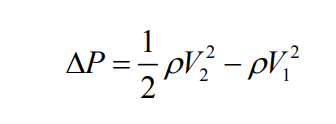
From continuity we can substitute the throat velocity (V2) out of the above equation, yielding the following:
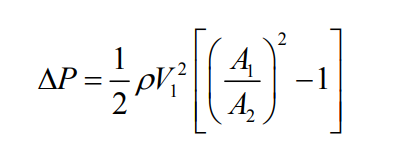
Solving for the upstream velocity and multiplying by the cross sectional area gives the volumetric flow rate Q.
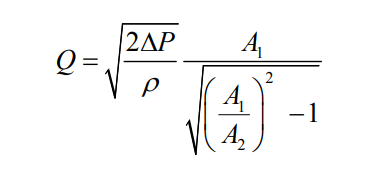
Ideal fluids would obey this equation, however small amounts of energy are converted into heat within the viscous boundary layers, and tend to lower the actual velocity of real fluids. A discharge coefficient C is typically introduced to account for the viscosity of the fluid.

C is found to depend on the Reynolds Number of the flow, and usually lies between .90 and .98 for smoothly tapering venturis.
For air flow you can use the same calculation and assume that the gas is incompressible. The density needs to be adjusted appropriately using the ideal gas formula.
Credits - Mitchell Cottrell