Relay Based Tuning Controller
Another way to make a process oscillate is to use a control system which is intrinsically oscillatory. An on-off control system has this property, which is why it is seldom used in chemical process control.
However, restricting the size of change which the controller can produce will restrict the amplitude of the oscillations. These can thus be small enough not to upset the process, or its operators!
This controller has a parameter deadzone , which defines the minimum change in the measured variable required to produce a change in output. The other parameter defines the size of the output of the controller. This is set to be + output/2 when the controller is on and - output/2 when it is off.
The algorithm for the on-off controller is as follows.
error = setpoint - measurement if (error>deadzone) adjustment = output / 2 if (error<deadzone) adjustment = - output /2
The size of output can be quite small, although it must be enough to swing the measured variable across the range of the deadzone. This latter must be larger than any noise in the process.
This controller will oscillate at a period equal to Pu . (Actually if the output is too close to the value required to swing the measurement across the whole deadzone, the period will be slightly longer. It should be enough to cover 4 or 5 times the deadzone.)
If the observed amplitude of the oscillations (maximum to minimum) is a the ultimate gain of the process can be shown to be:
![]() = (4 * output ) / (
= (4 * output ) / ( ![]() * a)
* a)
Example of Relay Based Controller Tuning
We can use the above algorithm in an actual experiment. In the example below the first order process parameters are:
- Delay time = 5
- Time constant = 20
- Gain = 3.5
Other information required by the program is a value for the controller deadzone = 0.01.
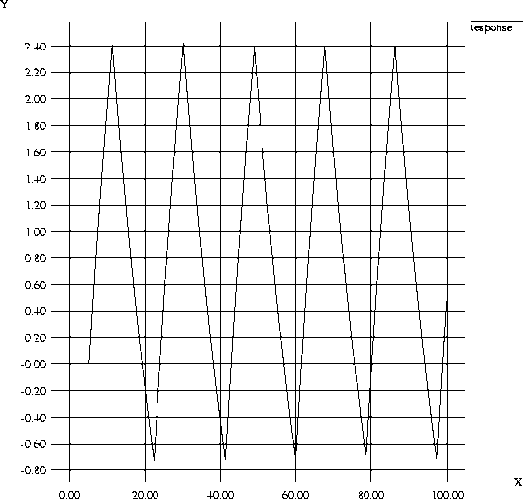
Now let us run the experiment with the output of the controller restricted to 4. This gives the following response.
From this response we can determine the value of a, the observed amplitude of the oscillations and the period of oscillation.
- a = 3.1
- Pu = 19
and hence evaluate the ultimate gain and the tuning parameters.
-
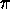 = (4 * 4)/(
= (4 * 4)/(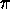 * 3.1) = 1.64
* 3.1) = 1.64
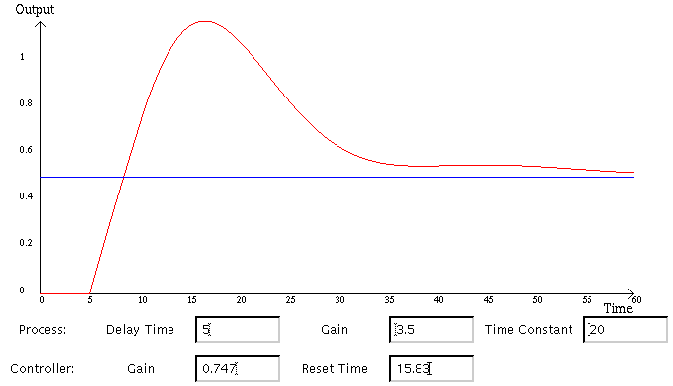
- Controller gain = 0.747
- Controller reset = 15.83
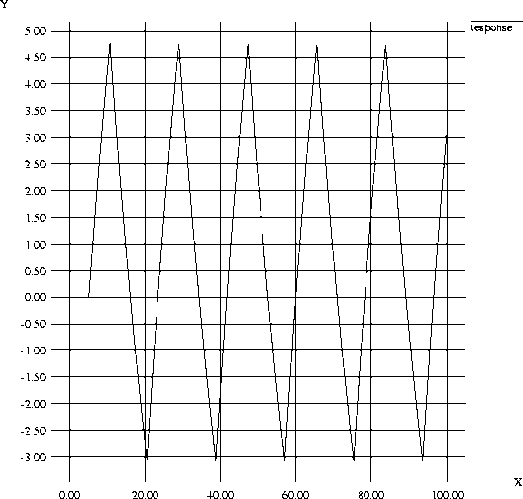
Now let’s try the same process again this time restricting the controller output to 10.
From this response we can determine the value of a, the observed amplitude of the oscillations and the period of oscillation.
- a = 7.75
- Pu = 19
and hence evaluate the ultimate gain and the tuning parameters.
-
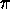 = (4 * 10)/(
= (4 * 10)/(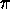 * 7.75) = 1.64
* 7.75) = 1.64
- Controller gain = 0.747
- Controller reset = 15.83
As you can see the two examples give the same values for the tuning parameters. How well do these values actually control the process at a setpoint of 0.5?
This approach can form the basis of a self tuning controller which is switched into on-off or relay mode to determine Pu and ![]() and hence tuning parameters which then get set into the controller.
and hence tuning parameters which then get set into the controller.