It basically depends on two things that are: the system input and the system order
For temporary response in first order plants we have:
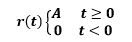
His Laplace transform is:
TEMPORARY RESPONSE OF CONTROL SYSTEMS SYSTEMS
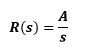
And the system model is:
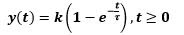
TEMPORARY RESPONSE OF CONTROL SYSTEMS
The above equation is the general expression of an output for a first-order system before unit step input
Being the system
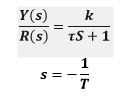
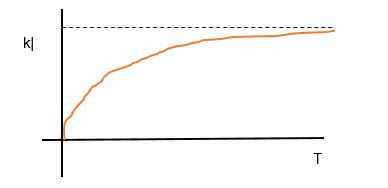
Graphically.
If R (s) = 1 / s is a unit step.
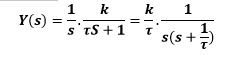
Applying inverse Laplace transform,
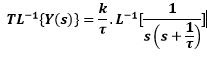
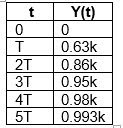
From T to 2T the state behaves as transitory and the effect of the pole is quite considerable
TEMPORARY RESPONSE OF CONTROL SYSTEMS
From 3T to 5T the state is stationary. The effect of the pole disappears over time
SYSTEM CARACTERISTICS
VALUE OF THE OUTPUT IN STABLE STATE (Yee) is the value that the output takes and (t) when
T tends to infinity
yee = k
CONSTANT OF TIME (T): is the time it takes to reach 63.2% of the output in a stable state of yee
ESTABLISHMENT TIME (ts) time it takes to reach yee at 4T or 5T
EXAMPLE: for the following system before a unit step and step six magnitude input must be determined.
a) Time constant
b) Establishment time
c) Value of the output in stable state
d) Mathematical expression of the output
e) Graphical representation of the output and location of poles
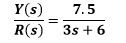
SOLUTION
1 the equation is normalized by dividing by 6
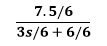
Dividing by 6 which corresponds to the magnitude and step 6 we have the model as follows:
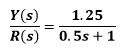
Therefore, the time constant is 0.5sec
Establishment times are 4T or 5T

The value of the steady state output yee = 1.25
Mathematically speaking we can solve the system as follows:
a = 6
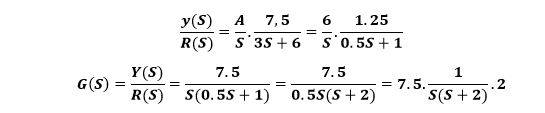
Applying inverse laplace transform is as follows:
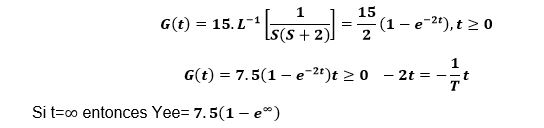
The response to a unit ramp is as follows:

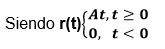
If A = 1 before a unit ramp system, the behavior of the system is as follows:

If A = 1
So;
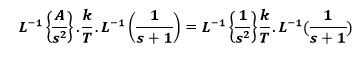
UNIT RAMP INPUT
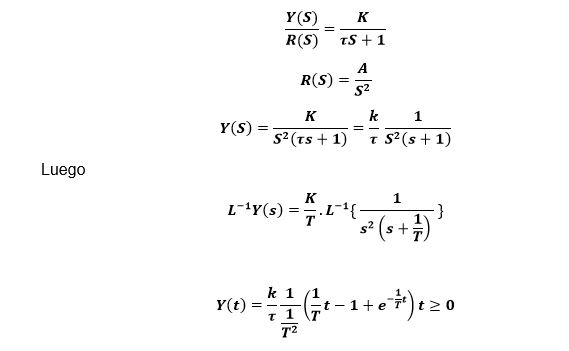
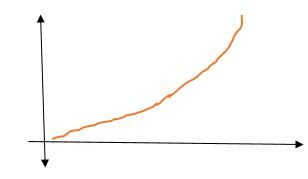
if the amplitude of the input is changed
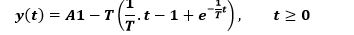
TEMPORARY RESPONSE OF SECOND ORDER SYSTEMS.
A second order system has the following equation as a transfer function:
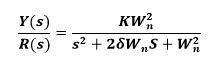
Where;

The steady state gain corresponds to the constant value that the system takes for a very large time
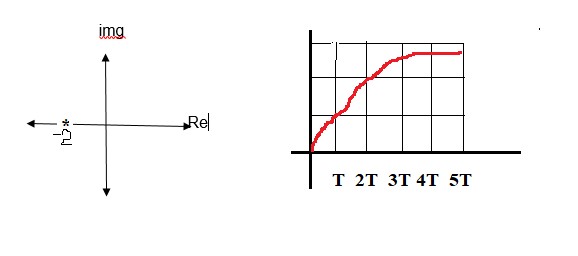
In addition, the response of the system depends on the roots of the denominator (system poles) for a second order plant, the poles are expressed as:
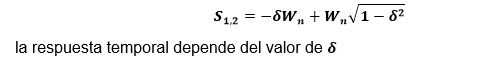


The poles and the output of the system are represented as follows


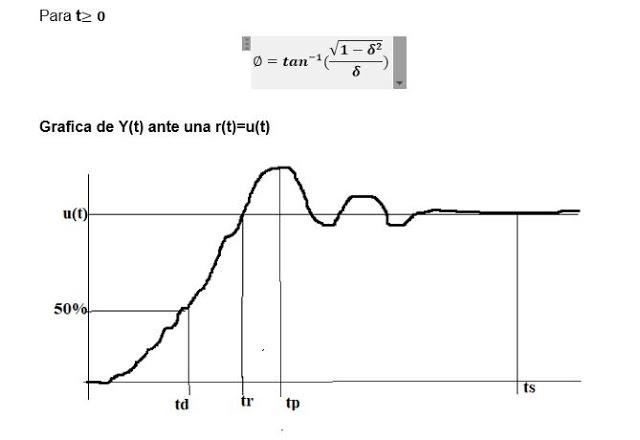
(td) delay time = time it takes for the first time to reach 50% of yee
(TR) growth time = is the time elapsed until the output changes from 0 to 100% of yee ie: yee = k
(tp) peak time = time in which ymax reaches its maximum value
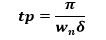
ts) establishment time = Time elapsed until the output reaches an approximate range of 2% or 5% of yee
For a criterion of 2%