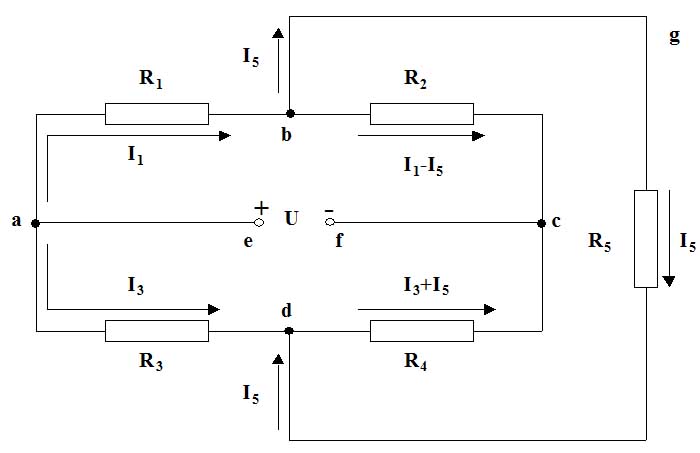
Below I give you the derivation of the balanced condition for a Wheatstone bridge. Figure shows a circuit of five electrical resistors connected to form the Wheatstone bridge.
Figure .: Wheatstone bridge.
Here we use two Kirchoff’s Laws. The first Kirchoff’s law says: the total current flowing into any junction is equal to the total current flowing out of this junction. The second Kirchoff’s law states: the total change in potential around any closed circuit loop is equal to zero.
For the second Kirchoff’s law we should be sure to include the sign of potential energy correctly: the potential decreases around a resistor in the direction of current flow and increases in the direction opposite to current flow; potential increases from negative to positive terminals of the battery.
Below I give you two different methods for the derivation of the balanced condition for a Wheatstone bridge.
Now, let’s consider several closed circuit loops and apply the above law to them.
- Loop e-a-b-c-f-e :
![]()
equation 4
- Loop a-b-g-d-a
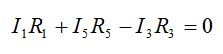
equation 5
- Loop b-c-d-g-b
![]()
equation 6
Here, U is a dc voltage, and U≠ 0.
So, we have three equations with 3 unknowns - I1; I3 and I5.
![]()
equation 7
![]()
equation 8
![]()
equation 9
Now we combine terms with I1; I3 and I5.
![]()
equation 10
![]()
equation 11
![]()
equation 12
Now we evaluate the determinant of the matrix developed using this set of equations:
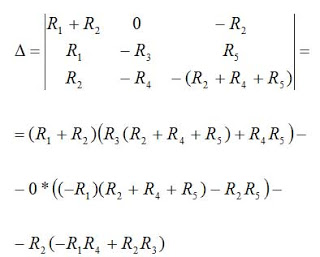
equation 13
In the case of the Wheatstone bridge the resistance R5 is substituted by an ampmeter. Ampmeters have a negligibly small resistance, so we can write that R5 = 0. With this condition we can re-write (13) as follows:
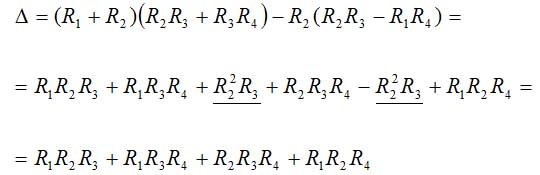
equation 14
Because all Ri > 0 we have that ∆ > 0 and ∆ ≠ 0.
For current I5 we have:
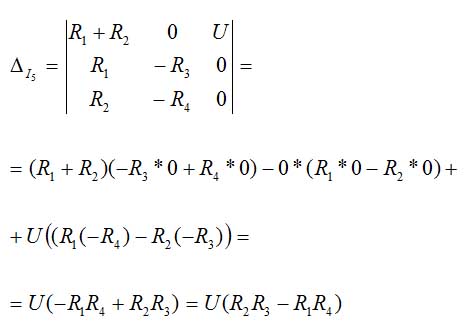
equation 15
Now we can evaluate the value of the current, which flows through an ammeter as follows:
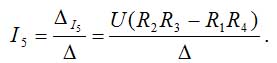
equation 16
We know that a balanced condition is when current I5 = 0, and because ∆ > 0, and ∆ ≠ 0 and U ≠ 0, we can give an expression for the balanced condition for the Wheatstone bridge as follows:
![]()
equation 17
or, finally,
![]()